Mathematics
Трев Ж.. Лекции по линейным уравнениям в частных производных с постоянными коэффициентами.. 1965
Description: Библиотека сборника математика М. Изд-во Мир. 1965г. 296с. Мягкий переплет, обычный формат. Книга посвящена общей теории дифференциальных уравнений в частных производных с постоянными коэффициентами. Главное внимание уделяется локальным свойствам решений, построению и исследованию различных фундаментальных решений, а также разрешимости в целом. Дано обстоятельное введение в широкий круг современных исследований, в большой степени интересных не только для математиков. Изложение в основном доступно студентам средних курсов Физико-математических факультетов.
Макки Дж.. Лекции по математическим основам квантовой механики. 1965
Description: Серия "Библиотека сборника "Математика". М., Мир, 1965 г. 222 с. Cостояние отличное.
Рождественский Б.Л.. Лекции по математическому анализу. . 1972
Description: М. Наука 1972г. 544с. Твердый издательский переплет, Обычный формат. Основное внимание уделяется глубокому изложению основных понятий анализа и методов качественного исследования. В связи с запросами вычислительной математики широко освещаются методы приближенных вычислений, основанные на теоремах и понятиях математического анализа.
Попов Ю.П., Пухначев Ю.В.. Математика в образах.. 1989
Description: Научно-популярное издание. М.: Знание 1989г. 208 с. Палiтурка / переплет: Мягкий, обычный формат. Математические формулы - лишь удобный язык для изложения идей и методов математики. Сами же эти идеи и методы можно описать, используя привычные и наглядные образы из окружающей жизни. Следуя этому принципу авторы в доступной и увлекательной форме излагают основные понятия теории множеств, числовых рядов, дифференциального и интегрального исчисления и других разделов математики. Книга рассчитана на слушателей народных университетов естественнонаучных знаний и широкий круг читателей.
Румшиский Л.З.. Математическая обработка результатов эксперимента. 1971
Description: М.: Наука, Физматлит, 1971. — 192 с. Настоящее справочное руководство имеет своей целью дать экспериментатору необходимые сведения по основным методам обработки и анализа результатов опыта. Все рекомендации сопровождаются примерами их практического применения с указаниями об экономных методах расчета. Книга весьма полезна для начинающих знакомство с различными методами статистического анализа собираемых данных.
Соминский И.С.. Метод математической индукции.. 1955
Description: Серия: Популярные лекции по математике. Выпуск 3. Издание 3-е. М.: Гостехиздат 1955г. 48 с. Палiтурка / переплет: Мягкий, обычный формат. Для учащихся старших классов, студентов младших курсов педвузов, университетов, втузов. Может быть использована в школьном математическом кружке. С о д е р ж а н и е. Введение. Метод математической индукции. Примеры и упражнения. Доказательство некоторых теорем элементарной алгебры методом математической индукции. Решения.
Description of seller: следы воды
Федорюк М.В.. Метод перевала. . 1977
Description: Главная редакция физико-математической литературы. М. Наука 1977г. 368 с. Палiтурка / переплет: твердый, увеличенный формат. В книге рассмотрены основные методы асимптотических оценок интегралов, содержащих большой параметр: метод Лапласа, метод стационарной базы, метод перевала, как в одномерном, так и в многомерных случаях.
Тихонов А.Н., Арсенин В.Я.. Методы решения некорректных задач. . 1974
Description: Изд. 2-е, перераб. и доп. Учебное пособие для студентов вузов, обучающихся по специальности Прикладная математика. М. Наука 1974г. 288 с. Палiтурка / переплет: твердый, обычный формат. Книга посвящена методам построения устойчивых приближенных решений широкого класса некорректно поставленных математических задач. К этому классу задач относится большой круг так называемых обратных задач, к которым приводят проблемы обработки и интерпретации экспериментальных наблюдений. Освещаются вопросы нахождения обобщенных решений обратных задач, так как в классической постановке эти задачи могут не иметь решений.
Гальперин Г.А., Толпыго А.К.. Московские математические олимпиады.. 1986
Description: Книга для учащихся. Под ред. А.Н.Колмогорова. М. Просвещение 1986г. 303 с., илл. Палiтурка / переплет: твердый,,,, увеличенный формат. Книга содержит задачи всех московских математических олимпиад за 50 лет их проведения. К большинству задач даны ответы, указания, решения. В книге много интересных задач, связанных с современными научными проблемами. Книга предназначена для учащихся VII-X
Бубенников А. В., Громов М. Я.. Начертательная геометрия.. 1973
Description: Учебник. М. Высшая школа 1973г. 416 с., ил. твердый переплет, увеличенный формат. В учебнике изложены вопросы построения чертежей простейших геометрических образов - точек, прямых, плоскостей. Даны схемы решения позиционных задач основным способом и способами преобразования эпюра Монжа. Рассмотрены виды многогранников, плоские и пространственные кривые линии, поверхности основных видов и сложных форм. Указаны графические методы определения площадей кинематических поверхностей и методы определения объемов тел, ограниченных поверхностями; даны понятия о кривизне поверхностей.
Касаткин В.Н.. Необычные задачи математики. . 1987
Description: К. Радянська школа, 1987г. 128 с. Твердый переплет.,, уменьшенный формат. В книге с помощью системы занимательных задач раскрываются математические основы теории автоматов. Значительное внимание уделяется алгебре логики и теории графов.
Бом Д.. Общая теория коллективных переменных.. 1964
Description: Перевод с английского. Серия: `Теоретическая физика`. М.: Мир, 1964г. 152 с. мягкий переплет, Обычный формат. Настоящая книга представляет собой перевод курса лекций известного физика-теоретика Д. Бома, прочитанных в летней школе теоретической физики в Лезуш (Франция). Читателям уже знакома ранее вышедшая книга Д. Бома `Квантовая теория` (Физматгиз, 1961 г.). Предлагаемые лекции содержат систематическое изложение одного из методов теоретического исследования системы заряженных частиц, а именно метода коллективных переменных, широко применяемого, в частности, в физике твердого тела и физике плазмы. В книге рассматриваются в основном классические системы, хотя затрагиваются также и квантовые (ферми-системы). В целом книга рассчитана на физиков - как теоретиков, так и экспериментаторов, желающих познакомиться с этим методом и облегчить себе изучение оригинальных журнальных статей.
Яворский, И. В.. Отображение симметрии физического пространства в пространстве Фурье . 1964
Description: (Расчетные таблицы)И. В. Яворский. - М. : Высш. шк., 1964. - 176 с
Каплан И.А.. Практические занятия по высшей математике.. 1965
Description: (Аналитическая геометрия на плоскости и в пространстве, дифференциальное исчисление функций одного и многих переменных) Изд-е 2-е, доп. и перер. Учебник для технических вузов Харьков Издательство Харьковского университета 1965г. 575 с. Палiтурка / переплет: Твердый, Слегка увеличенный формат.
Каплан И.А.. Практические занятия по высшей математике. Часть III.. 1965
Description: Харьков. Издательство Харьковского университета. 1965г. 376с. Палiтурка / переплет: твердый,, увеличенный формат. Интегральное исчисление функций одной независимой переменной. Интегрирование дифференциальных уравнений.
Каплан И.А.. Практические занятия по высшей математике. Часть V. . 1972
Description: Харьков Харьковского ордена трудового красного знамени гос. Ун-та им. Горького . Палiтурка / переплет: Тканевый корешок, картонный, увеличенный формат. (Продавец: BS - ЛЬВІВ, Львів.) Цена: 950 грн. Купить Численное решение алгебраических и трансцендентных уравнений, матричное исчисление, векторный анализ и интегрирование линейных дифференциальных уравнений первого порядка с частными производными. 1972 г. 412 с.
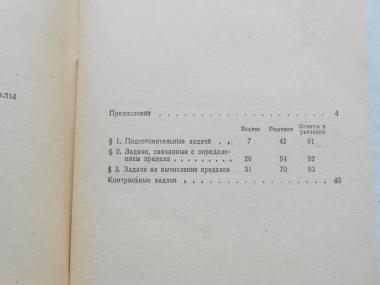
Кириллов А.А.. Пределы. . 1973
Description: Серия: Библиотечка физико-математической школы. Выпуск 2. Издание второе, переработанное. М. Наука 1973г. 96 с., илл. Палiтурка / переплет: мягкий, обычный формат. Книга состоит из задач: подготовительных, связанных с определнием предела, на вычисление пределов. Книга может служить учебником по теме ``Пределы``. При составлении книги автор широко пользовался ``математическим фольклором``.
Расулов М.Л.. Применение метода контурного интеграла. 1975
Description: к решению задач для параболических систем второго порядка. М. Наука 1975г. 256с. твердый переплет, Обычный формат. Монография состоит из двух частей. Первая посвящена систематическому изложению разработанного автором вычетного метода и его применению к решению широких классов задач дифференциальных уравнений, не поддающихся решению известными методами. Во второй части дается новый метод, названный методом контурного интеграла, в применении к исследованию весьма общих линейных смешанных задач дифференциальных уравнений.
Пайнс Д.. Проблема многих тел. . 1963
Description: М. ИЛ 1963г. 190с. мягкий переплет, Обычный формат. Настоящая книга представляет собой развернутый обзор статистической теории систем многих частиц и применяемых в ней методов исследования, в особенности методов, связанных с исследованием уравнений движения и функций Грина. Из приложений рассмотрены неидеальные ферми- и бозе системы, причем автор уделяет основное внимание не столько деталям расчета того или иного эффекта, сколько обсуждению физической стороны вопроса, целесообразности того или иного подхода, справедливости выбранного приближения и получаемых с его помощью результатов и т.д.
Каплан Я.Л. Рівняння. . 1968
Description: Серія: `Бібліотека вчителя математики`. К.: Радянська школа, 1968г. 406 с. твердый переплет,, Обычный формат. У цій книжці наведено основні відомості про рівняння, пояснено причини появи сторонніх і втрати справжнів коренів рівняння. Розрахована на вчителів середньої школи.
Кириченко Ю.В., Кириченко С.Ю., Омельченко В.И. и др.. Репетитор по математике для поступающих в вузы. 1998
Description: Учебное пособие для поступающих в технические и экономические вузы. Харьков: Фолио, Ростов: Феникс 1998г. 463 с. Палiтурка / переплет: Ламинированный тверд., обычный формат. Алгебра, тригонометрия, геометрия. Необходимые теоретические сведения, основные методы решения задач с большим количеством разобранных примеров, задачи для самостоятельной работы.
Горнштейн П., Поляк Н., Тульчи.. Решение конкурсных задач по математике. (М.И. Сканави.). 1992
Description: Горнштейн П., Поляк Н., ТульчиРешение конкурсных задач по математике нский В. из сборника под редакцией М.И. Сканави. Группа В. Киев РИА Текст, МП ОКО 1992г. 246 с. Палiтурка / переплет: Мягкий, обычный формат. В пособии содержатся решения задач повышенной трудности из известного `Сборника конкурсных задач по математике для поступающих во втузы` под редакцией М.И. Сканави. Для абитуриентов, слушателей подготовительных курсов, преподавателей математики, репетиторов.
Романовский П.И.. Ряды Фурье. Теория поля. Аналитические и специальные функции. Преобразование Лапласа. . 1964
Description: Романовский П.И. Ряды Фурье. Теория поля. Аналитические и специальные функции. Преобразование Лапласа. Издание 4-е. Избранные главы высшей математики для инженеров и студентов ВТУЗов М. Физматгиз 1964г. 304 с. Палiтурка / переплет: Твердый, Обычный формат.
Кручкович Г.И., Мордасова Г.М. и др.. Сборник задач и упражнений по специальным главам высшей математики.. 1970
Description: Учеб.пособ.для втузов. Под ред. Г.И. Кручковича М. Высшая школа 1970г. 512 с. Палiтурка / переплет: Твердый, Слегка увеличенный формат. Сборник включает теоретические сведения, задачи и упражнения по следующим спецглавам курса ВМ: матричное исчисление, скалярные и векторные поля, ФКП, специальные функции, преобразования Фурье, операционное исчисление, уравнения математической физики, основы теории вероятностей. Типовые задачи даны с подробными решениями и пояснениями. Приведены задачи для упражнений. К отдельным задачам даются методические указания.